Path Following

February 03, 2015

I’ve written before about splines, it was mostly a historical intro. So today I want to delve into technical details. The animation system uses splines extensively (the path of the players are defined by splines). We have made a simple editor that let the artist control the trajectory of the players. After defining the trajectory, the artist can control the speed of the player along the path using a unity curve field.

Defining paths with local tension, continuity, and bias control

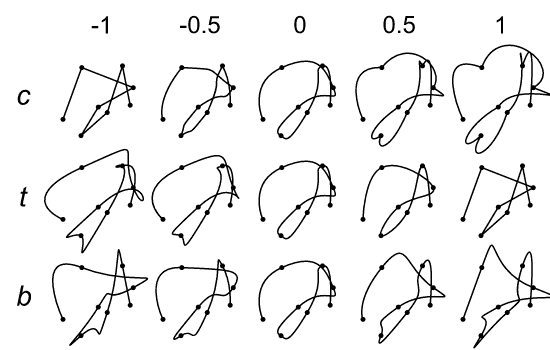
You can notice that the curve goes through all the control points (unlike bezier curves). The designer is allowed to define the path by the target points without explicitly manipulating the tangents. This particular type of splines is called Kochanek–Bartels spline. They have three parameters : tension, bias, and continuity that change the appearance of the path. The image below shows the change in the curve appearance when varying the different parameters. c = continuity, t = tension and b = bias.

Implementation Details

As we have seen, tangents are manipulated implicitly with tension, bias, and continuity. And the path goes through all the control points. The normals are automatically generated using those parameters and then we interpolate the position using hermite spline.

\phi(t) = (2t^3 - 3t^2 + 1) \cdot p_0 + (t^3 - 2t^2 + t) \cdot m_0 + (-2t^3 + 3t^2) \cdot p_1 + (t^3 - t^2) \cdot m_1

p0 : first control point. p1 : second control point. m0 : tangent at p0. m1 : tangent at p1.

The high level code :

// Returns the control point at index
Vector3 p0 = GetPoint(index);
// Calculate the corresponding tangent
Vector3 m0 = GetTangent0(index);
// Returns the next control point
Vector3 p1 = GetPoint(index + 1);
// Calculate the corresponding tangent
Vector3 m1 = GetTangent1(index + 1);
position = HermiteCurve(s, p0, m0, p1, m1);

So basically we need to calculate the tangent for the two control points and then use the Hermite interpolation. The first tangent is defined as bellow.

private Vector3 GetTangent0(int i)
{
   if (i == 0)
   {
       return 0.5f * (1 - tension) * (1 - bias) * (1 - continuity) * (GetPoint(i + 1) - GetPoint(i));
   }
   if (i == Points.Length - 1)
   {
       return 0.5f * (1 - tension) * (1 + bias) * (1 + continuity) * (GetPoint(i) - GetPoint(i - 1));
   }
   return 0.5f * (1 - tension) * (1 + bias) * (1 + continuity) * (GetPoint(i) - GetPoint(i - 1)) +
           0.5f * (1 - tension) * (1 - bias) * (1 - continuity) * (GetPoint(i + 1) - GetPoint(i));
}

The second tangent is calculated using the formula :

private Vector3 GetTangent1(int i)
{
   if (i == 0)
   {
       return 0.5f * (1 - tension) * (1 - bias) * (1 + continuity) * (GetPoint(i + 1) - GetPoint(i));
   }
   if (i == Points.Length - 1)
   {
       return 0.5f * (1 - tension) * (1 + bias) * (1 - continuity) * (GetPoint(i) - GetPoint(i - 1));
   }
   return 0.5f * (1 - tension) * (1 + bias) * (1 - continuity) * (GetPoint(i) - GetPoint(i - 1)) +
           0.5f * (1 - tension) * (1 - bias) * (1 + continuity) * (GetPoint(i + 1) - GetPoint(i));
}

And finally the Hermite interpolation function :

private static Vector3 HermiteCurve(float t, Vector3 p0, Vector3 m0, Vector3 p1, Vector3 m1)
{
   return ((2.0f * t * t * t - 3.0f * t * t + 1.0f) * p0 +
           (t * t * t - 2.0f * t * t + t) * m0)
               + (((-2.0f * t * t * t + 3.0f * t * t) * p1) +
               ((t * t * t - t * t) * m1));
}

Calculating the tangent at a point in the path In order to orient the player along the path we need to calculate the tangent in an arbitrary point in the curve. The curve is a function that takes a parameter t between 1 and 0 and returns a position (a 3d vector).

$\phi(t) : [0,1] \to \mathbb{R}^3$

If we calculate the derivative of the curve at a particular point we obtain a tangent.

We obtain :

Back to code, lets wrap the formula in a function :

private static Vector3 HemiteCurveTangent(float t, Vector3 p0, Vector3 m0, Vector3 p1, Vector3 m1)
{
   return m0 * (3.0f * t * t - 4.0f * t + 1.0f) + t * (m1 * (3.0f * t - 2) + 6.0f * (t - 1.0f) * (p0 - p1));
}

Reparametrization of Kochanek–Bartels splines

In the next article we will talk about the reparameterization of the path. This is very useful if you want to control the speed of moving along the path or you want to sample points in the path at equal distances.